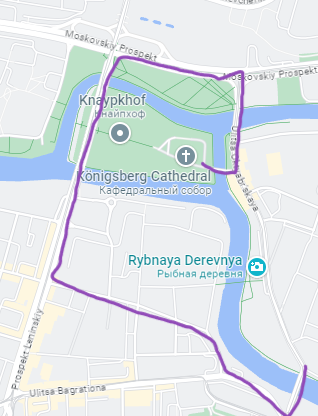
Will Hunting's Solution
> The scene from the movie:
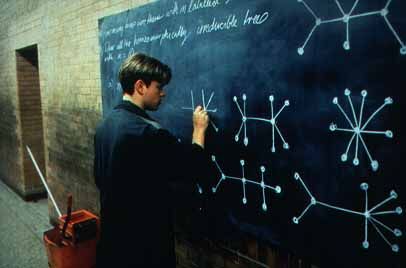
> The scene from the movie:

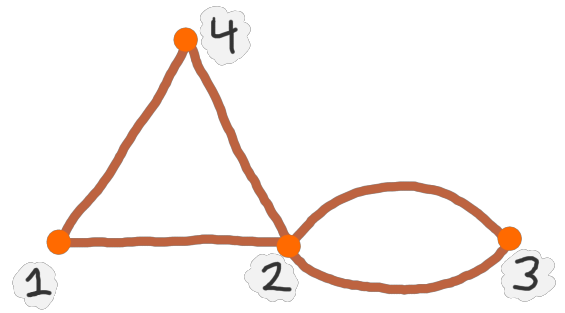
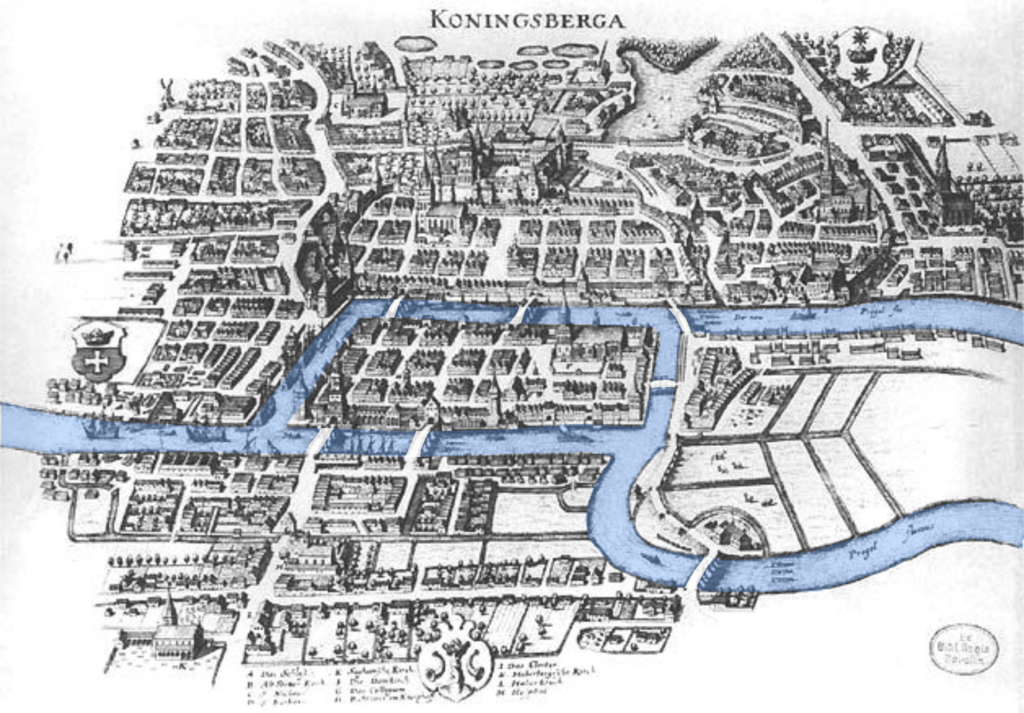
> Sorry, it's impossible! However, during WWII, the city was bombed, causing two of the bridges to be destroyed. Now, Königsberg has been renamed Kaliningrad. A recent map of Kaliningrad (rendered in 2023) is below.
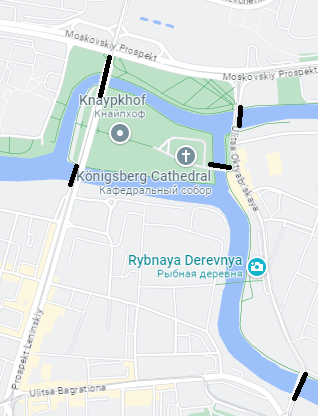
> Here's how you could cross these five bridges on your next vacation: